Cet article tend à justifier et mettre en avant l’utilisation de méthode hybride reliant modèle non-linéaire pour raffiner et simplifier les données avant de les transmettre à des modèles plus simples d’interprétation.
Contexte
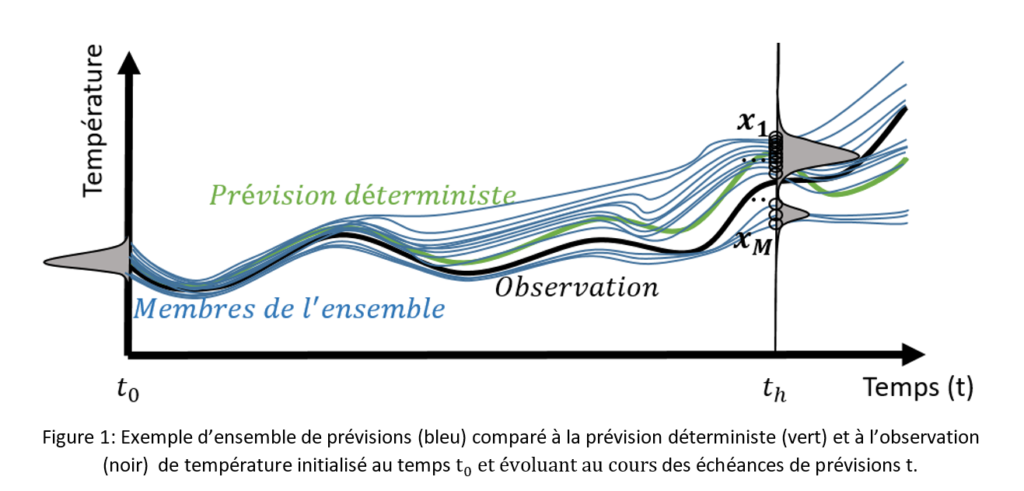
De nos jours, la prévision météorologique déterministe est d’une importance économique reconnue. Issue numériquement de modèles d’approximation d’états de l’atmosphère, la prévision est soumise à d’importantes erreurs évoluant suivant les échéances de prévisions. Afin de quantifier la distribution de l’incertitude autour des prévisions, des ensembles des trajectoires (membres) sont générés en perturbant les conditions initiales et le modèle atmosphérique (voir figure 1).
Les ensembles de prévisions sont également sujets aux erreurs de distribution provoquée par les phénomènes non-linéaires locaux difficiles à reproduire. De mauvaises estimations de la réelle variabilité régnant autour de la prévision déterministe peuvent entraîner le manque de représentation de scénarios extrêmes (fortes pluies, hausses importantes des températures, etc.) visité par l’observation météorologique. Dans le but de rendre la distribution des ensembles plus fiable, la communauté scientifique propose d’appliquer des méthodes statistiques pour corriger les ensembles d’une variable météorologique (température, vitesse du vent, etc.) à l’aide des observations in situ. Parmi ces méthodes, la régression quantile est régulièrement appliquée pour répondre à l’objectif de prédiction d’un ensemble de valeur, contrairement à la régression classique avec un objectif de prédiction unique.
Modélisation hybride
À partir de ces prédictions de l’ensemble de valeurs issues de la régression quantile, il est possible d’obtenir la distribution corrigée de l’ensemble de prévisions étudiées. Une contrainte à ce problème est d’associer à un ensemble de quantiles croissants des valeurs. Cette contrainte assure le fait de retrouver une distribution correcte. Dans ce contexte, l’article propose d’approcher la fonction quantile par une combinaison linéaire de polynômes de Bernstein.
Cet outil mathématique permet d’estimer la fonction quantile en respectant la contrainte citée tout en étant simple et flexible. Cependant, ce modèle n’est pas adapté face à la grande dimensionnalité spatiale ajoutée à celle du nombre de membres composant l’ensemble et à la non-linéarité des relations présentes dans les données. De ce fait, l’idée pour surpasser ces limitations est d’utiliser un autre algorithme en amont du modèle linéaire : le réseau de neurones.
Le réseau de neurones a montré ces dernières années un grand potentiel de performances d’apprentissage dans les divers domaines. Ce type de modèle d’apprentissage fait régulièrement l’objet d’applications au travers de multiples domaines tels que la correction d’ensembles de prévisions. Néanmoins, le réseau de neurones souffre également d’un manque d’explicabilité de ces performances. Ce point pose une difficulté majeure pour les scientifiques dans la compréhension des phénomènes météorologiques importants pour corriger la distribution des ensembles.
Il est proposé dans cet article d’utiliser un modèle hybride (QRF) reliant un réseau de neurones en amont d’un modèle linéaire simple et flexible pour aider à réduire la complexité de l’information fournie en entrée.
Les données spatiales étudiées forment une grille non régulière rendant l’utilisation d’un réseau de convolution difficile sans harmonisation de la grille. Pour éviter d’avoir à appliquer un traitement superflu aux données, il est proposé d’utiliser un simple « multilayer perceptron » qui est une architecture de réseaux de neurones de référence ayant déjà fait ses preuves dans ce contexte de données. Le réseau prend ensuite les membres de l’ensemble de prévisions en entrée ainsi qu’un vecteur de poids lié à chaque station spatiale de la grille.
Pour terminer, l’article de Bremnes montre l’important gain de performance d’utilisation d’un modèle hybride comparé aux approches de références dans une application à la correction des ensembles de prévisions de vitesses de vent en Norvège.
Découvrez l’article de référence :
Ensemble Postprocessing using quantile function regression based neural networks and Bernstein Polynomials
Auteurs : John Bjornar Bremnes
Source : https://journals.ametsoc.org/view/journals/mwre/148/1/mwr-d-19-0227.1.xml
Parution le : 01/01/2020
Envie de rester informé(e) ?
Abonnez-vous à la Newsletter Scal[ia]